Bayesian Optimization over Discrete and Mixed Spaces via Probabilistic Reparameterization

Abstract

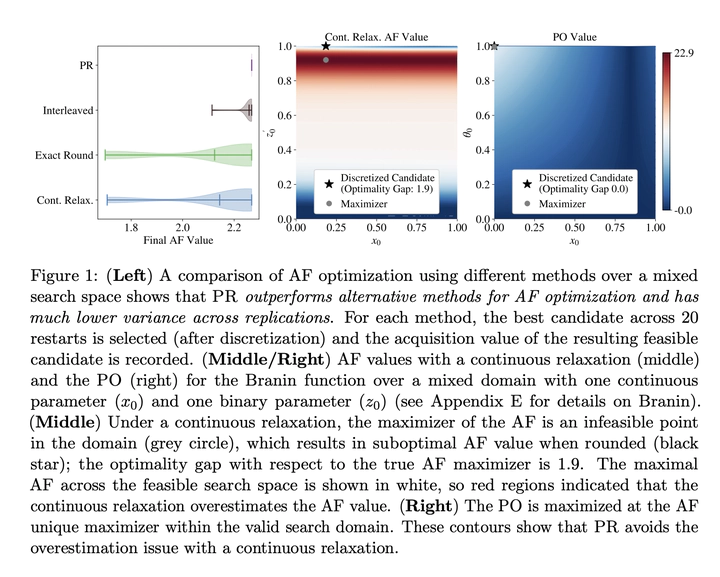
Optimizing expensive-to-evaluate black-box functions of discrete (and potentially continuous) design parameters is a ubiquitous problem in scientific and engineering applications. Bayesian optimization (BO) is a popular sample-efficient method that selects promising designs to evaluate by optimizing an acquisition function (AF) over some domain based on a probabilistic surrogate model. However, maximizing the AF over mixed or high-cardinality discrete search spaces is challenging as we cannot use standard gradient-based methods or evaluate the AF at every point in the search space. To address this issue, we propose using probabilistic reparameterization (PR). Instead of directly optimizing the AF over the search space containing discrete parameters, we instead maximize the expectation of the AF over a probability distribution defined by continuous parameters. We prove that under suitable reparameterizations, the BO policy that maximizes the probabilistic objective is the same as that which maximizes the AF, and therefore, PR enjoys the same regret bounds as the underlying AF. Moreover, our approach admits provably converges to a stationary point of the probabilistic objective under gradient ascent using scalable, unbiased estimators of both the probabilistic objective and its gradient, and therefore, as the numbers of starting points and gradient steps increase our approach will recover of a maximizer of the AF (an often neglected requisite for commonly-used BO regret bounds). We validate our approach empirically and demonstrate state-of-the-art optimization performance on many real-world applications. PR is complementary to (and benefits) recent work and naturally generalizes to settings with multiple objectives and black-box constraints.